Project:

Bi‑Directional Path Tracing

Author:

Dr. Iman Sadeghi

Instructor:

Prof. Henrik Wann Jensen

Venue:

CSE 272: Advanced Appearance Modeling Course, UC San Diego, Fall of 2017

Project Description:

In this project I focused on an advanced rendering technique called Bi Directional Path Tracing with Multiple Importance Sampling this technique somehow combines the classic Path Tracing algorithm with Light Tracing algorithm and exploits the benefits of both techniques. First I start by some rendered images and then I will describe some technical details.

Rendering Results Using Bi‑Directional Path Tracing with Multiple Importance Sampling

Diffuse Box - Caustics Scene


Diffuse Spheres - Empty Box

Rendering Results Using Naive Bi‑Directional Path Tracing with average weighting scheme

Diffuse Box - Caustics Scene

3D Geometry:

For Modeling I used try and error method to make the my Cornell Box look like the original Cornel Box. After spending hours working with Maya I made my box and it looked good. Then I realized that the data about the Cornell Box is available online! Which means I could save hours by just plugging in bunch of numbers! Anyways I think it was a good modeling practice and here you can see a comparison between my try-and-error-made model with the original Cornell Box.

Original Cornell Box (Photograph) - My Cornell Box (Model) - My Cornell Box (Rendered)

Rendering

Description of Path Tracing, Light Tracing and Bi‑Directional Path Tracing: Images are taken from [5]

Path Tracing


Path Tracing with next event estimate


Light Tracing


Light Tracing with next event estimate


Bi Directional Path Tracing

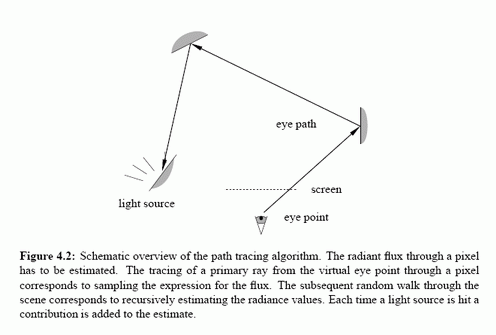
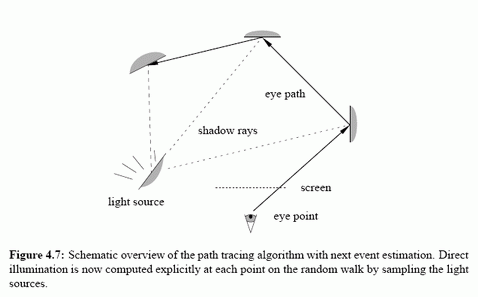
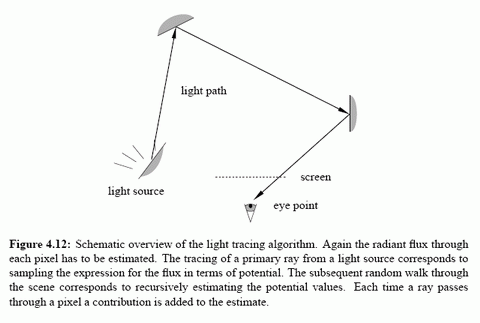
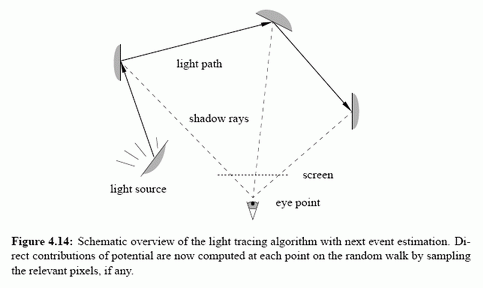
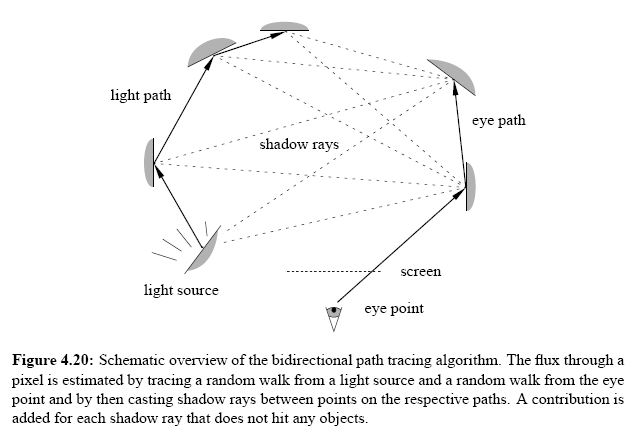
For the Multiple Importance Sampling part we have to assign the weights of the paths relative to the probobility of having that path in our sampling scheme. At the end the estimated flux per pixel would be:

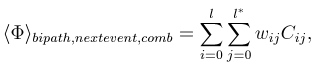
The only criteria here is that all the weights for paths of a given length sum up to one:

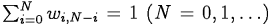
Any weighting that satisfies this condition would be an unbiased scheme which will converge to the final solution by increasing the number of samples.

For the Naive Bi Directional Path Tracing I used equal weights (1/n) for all the Wij of the same length. For implementing the Importance Sampling we should satisfy the following condition:

Bi‑Directional Path Tracing with Multiple Importance Sampling


Naive Bi‑Directional Path Tracing


Path Tracing


Light Tracing

Comparisons:

Naive Bi‑Directional Path tracing v. Bi‑Directional Path Tracing with Multiple Importance Sampling

Left: Naive Bi‑Directional Path Tracing with average weighting scheme between all the paths with same length
Center: Multiple Important Sampling with no special considerations
Right: Multiple Importance Sampling with considering special case of very short connecting path between eye-path and light-path.

Bi‑Directional Path Tracing (BDPT) v. Path Tracing (PT) v. Light Tracing (LT) v. Photon Mapping (PM)

Advantages:
Photon Mapping+
Path Tracing +
Light Tracing +
Bi‑Directional Path Tracing +


Disadvantages:
Photon Mapping+
Path Tracing +
Light Tracing +
Bi‑Directional Path Tracing +

Refrences:

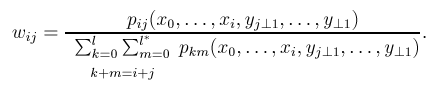
[1] Lafortune et al., Bidirectional Path Tracing", Compugraphics 1993
[2] Veach and Guibas, Optimally combining sampling techniques for Monte Carlo rendering, SIGGRAPH 1995
[3] Veach et al., Metropolis Light Transport, SIGGRAPH 1997
[4] Veach et al., Robust Monte Carlo Methods for Light Transport Simulation, Chapter 9 and Chapter 10
[5] Lafortune, Mathematical Models for Light Transport Simulation