Project:

Visualizing Mesh Curvature

Author:

Dr. Iman Sadeghi

Instructor:

Prof. Matthias Zwicker

Venue:

CSE291: 3D Geometry Processing Course, UC San Diego, Winter of 2008

Project Description:

The goal of this project is to learrn working with software libraries that provide many of the basic operations required for 3D geometry processing. For example VTK and CGAL. The goal is to computes principal curvature estimates at the mesh vertices and to visualize the curvatures using a color coding scheme.

For a two-dimensional surface embedded in R3, consider the intersection of the surface with a plane containing the normal vector and one of the tangent vectors at a particular point. This intersection is a plane curve and has a curvature. This is the normal curvature, and it varies with the choice of the tangent vector. The maximum and minimum values of the normal curvature at a point are called the principal curvatures, k1 and k2, and the directions of the corresponding tangent vectors are called principal directions.

Here we adopt the convention that Surface Curvature is taken to be positive if the curve turns in the same direction as the surface's chosen normal, and negative otherwise.

The Gaussian curvature, named after Carl Friedrich Gauss, is equal to the product of the principal curvatures, k1k2. It has the dimension of 1/length2 and is positive for spheres, negative for one-sheet hyperboloids and zero for planes. It determines whether a surface is locally convex (when it is positive) or locally saddle (when it is negative).

About VTK

The Visualization ToolKit (VTK) is an open source, freely available software system for 3D computer graphics, image processing, and visualization used by thousands of researchers and developers around the world. VTK consists of a C++ class library, and several interpreted interface layers including Tcl/Tk, Java, and Python. Professional support and products for VTK are provided by Kitware, Inc. VTK supports a wide variety of visualization algorithms including scalar, vector, tensor, texture, and volumetric methods; and advanced modeling techniques such as implicit modelling, polygon reduction, mesh smoothing, cutting, contouring, and Delaunay triangulation. In addition, dozens of imaging algorithms have been directly integrated to allow the user to mix 2D imaging / 3D graphics algorithms and data. The design and implementation of the library has been strongly influenced by object-oriented principles. VTK has been installed and tested on nearly every Unix-based platform, PCs (Windows 98/ME/NT/2000/XP), and Mac OSX Jaguar or later.

Software Code

The VTK package makess a lot of things (and not everything!) easier. For example to visualize the curvature you need only following lines of code:

vtkCurvatures *curv = vtkCurvatures::New();
	curv->SetInputConnection(norm->GetOutputPort());
	curv->SetCurvatureTypeToMean();
  
vtkPolyDataMapper *polyMap2 = vtkPolyDataMapper::New();
	polyMap2->SetInputConnection(curv->GetOutputPort());

Easy ha?! But the color coding is not very interesting! If you want to have a nice color coding you should also add the following lines to make a Lookup Table:

vtkLookupTable* lut=vtkLookupTable::New();
	lut->SetHueRange(0.0,0.6);		//Red to Blue
	lut->SetAlphaRange(1.0,1.0);
	lut->SetValueRange(1.0,1.0);
	lut->SetSaturationRange(1.0,1.0);
	lut->SetNumberOfTableValues(256);
	lut->SetRange(-100,100);
	lut->Build();

	polyMap2->SetLookupTable(lut);

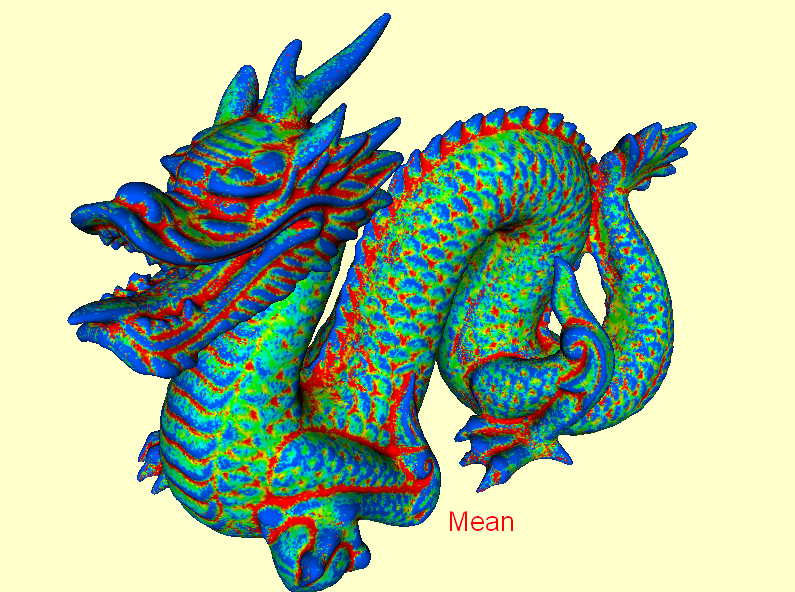
And the result is impressive, isnt it? But don't get too excited! ;)